Points Of Concurrency Worksheet Answers. Students want a compass, for this lesson. Students use a mnemonic system to remember the relationships between the altitude, orthocenter, medians, centroid, angle bisectors, incenter, perpendicular bisectors, and circumcenter. A sample question is answered, and two practice questions are supplied. A summary sheet for options and factors of concurrency for triangles, together with special properties formed by each.
Includes altitudes and orthocenter; angle bisector and incenter; median and centroid; perpemdicular bisector and circumcenter; and midsegment. Practice for geometry college students working on particular segments of triangles. Worksheet includes four triangles where college students will be tasked with discovering the coordinates of the circumcenter, orthocenter, or centroid.
Direct college students to finish this at residence tonight. They will be allowed approximately 10 minutes tomorrow to get back with their associate to Think-PairShare their options to this task after which turn in.
Print Factors Of Concurrency Worksheets
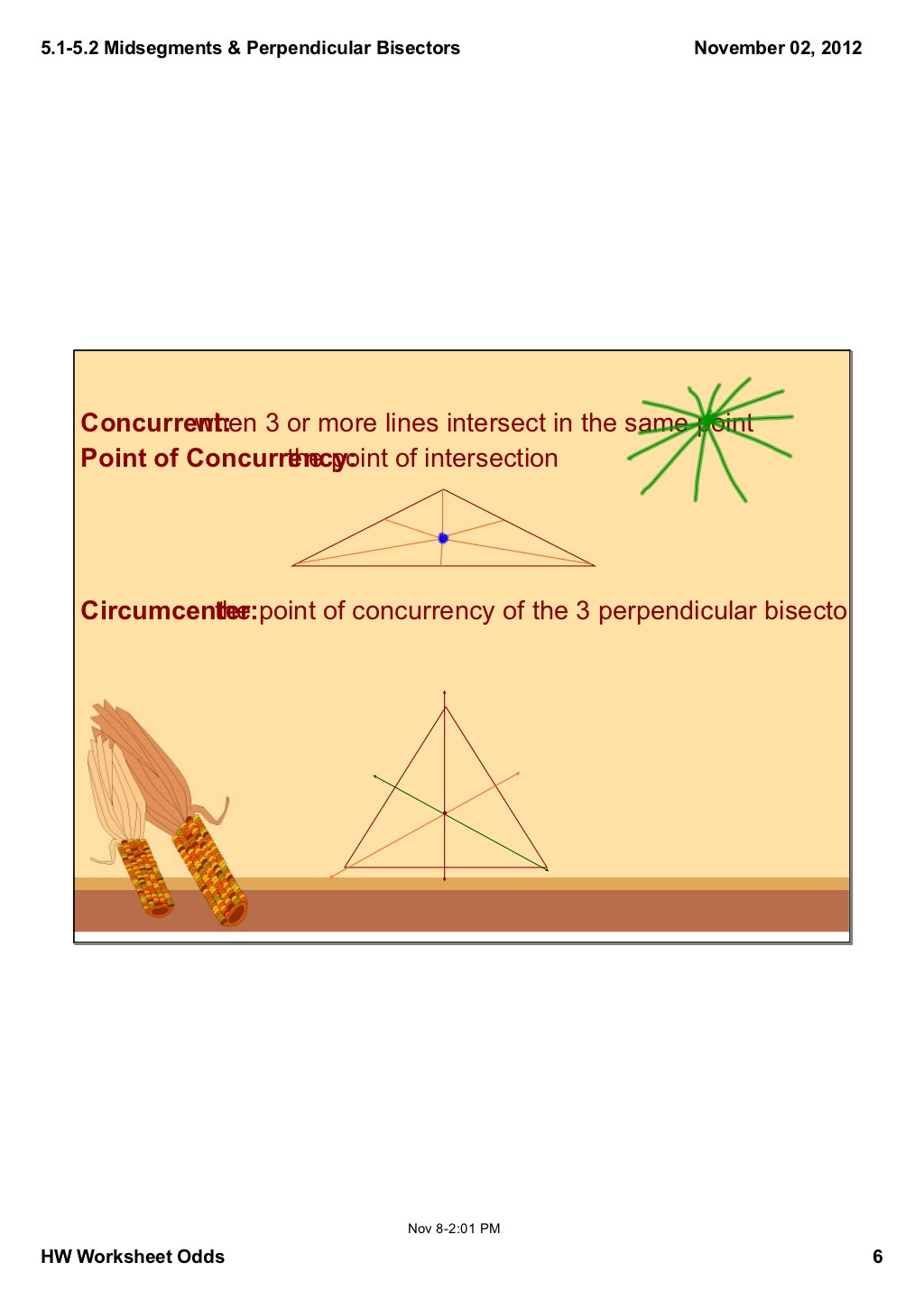
A level of concurrency is the purpose the place three or extra lines intersect at a single level. Over this assortment of worksheets you will use all of this geometric terminology. These worksheets explain concurrence.
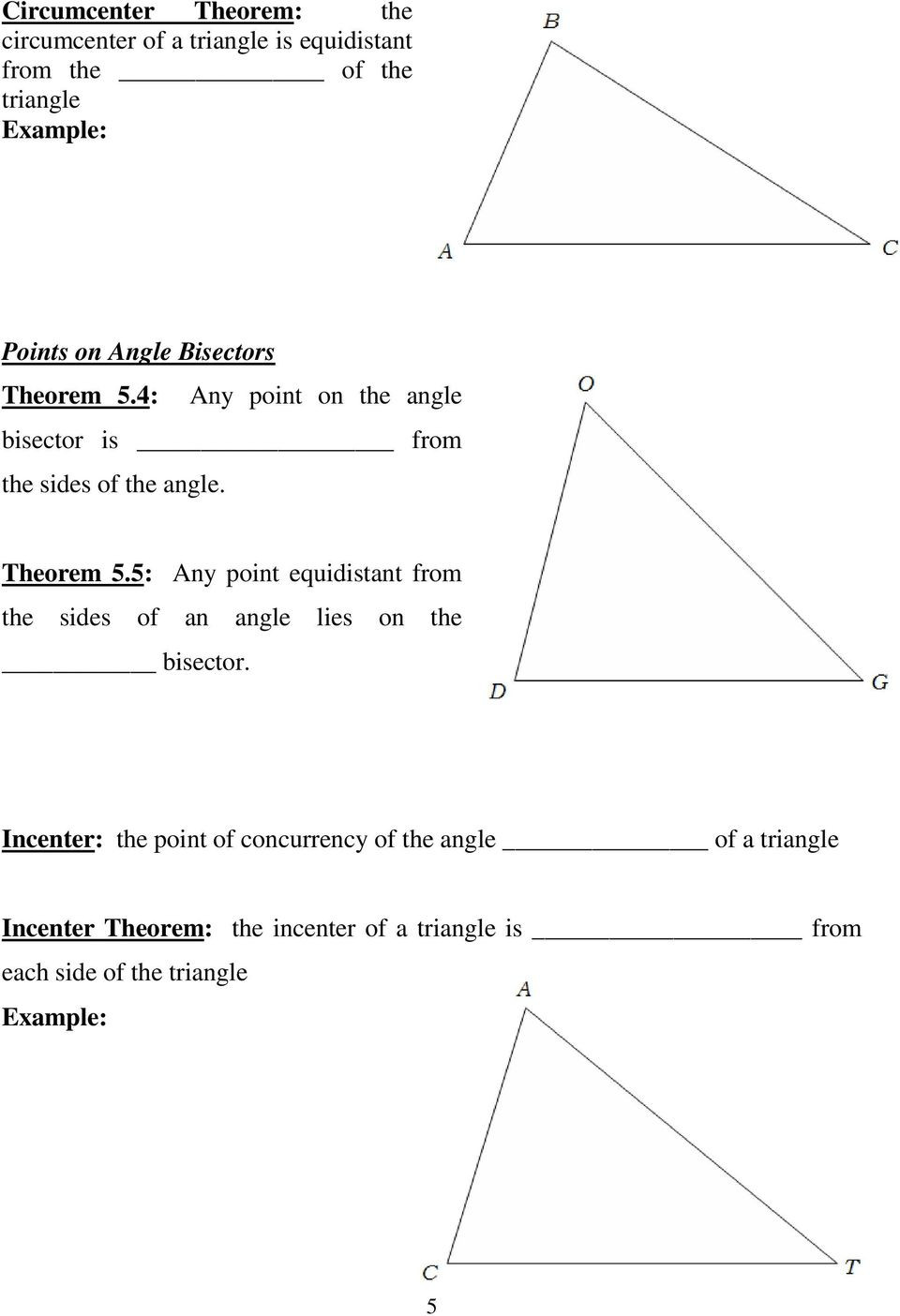
Students should finish the duty for homework if not accomplished in class. Students will answer questions primarily based off of this topic through the use of the visual help provided. Three questions are supplied, and house is included for school kids to repeat the proper answer when given.
Algebraic Geometry Math
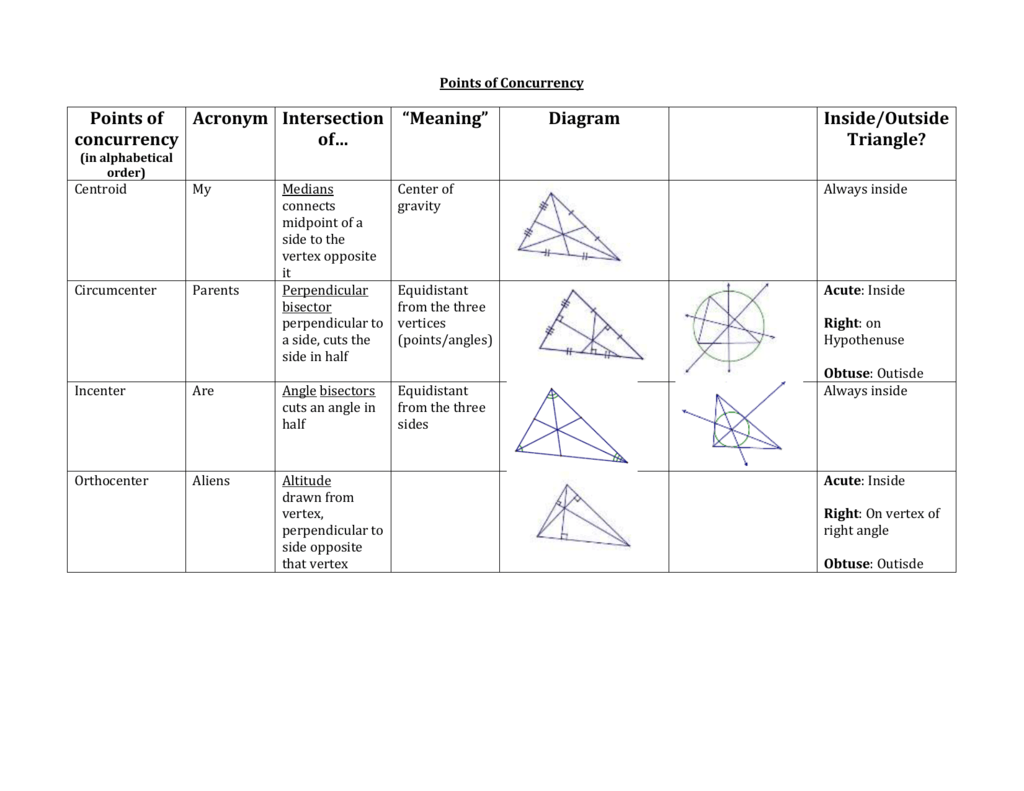
Orthocenter – The point of concurrency of the altitudes of a triangle. These worksheets will train your college students the proper terminology and calculations for factors of concurrency. The three medians of a triangle intersect on the ____________________.

It is only one level that we can share three or more lines. Constructed traces within the triangle’s inside are the most effective place the place you’ll be able to to find the points of concurrency. You construct a degree of concurrency for each of the next ones in a triangle; Medians, Perpendicular bisectors, Angle bisectors, Altitudes in a triangle.
Developing A Centroid: Arms On Math Exercise
Determine the gap from the airport location to each city. Describe a real-world application by which an understanding of concurrency in triangles would be an helpful problem solving tool. Target Practice Michael is in command of this year’s dart tournament at the native recreation middle.

Instead of using a circular dartboard he decided that it might be interesting to use a square dartboard with a triangle shaped middle as shown below. Points are awarded primarily based upon how close the dart is to the centroid of the triangle. The centroid is the purpose of concurrency of the medians of a triangle.
Using the four triangles connected that roughly represent the triangle shaped by Albany, Valdosta and Waycross, discover the centroid, incenter, circumcenter, and the orthocenter. You could choose from patty paper, MIRA, compass and straight edge, and Geometer’s Sketchpad to make your constructions. Choose a location for the tower based mostly on the work you did for query #2.

Triangle’s interior must not have two of the four points of concurrency whereas constructing the line segment as triangle’s half. Triangle’s centroid should always be current in between the triangle’s orthocenter and circumcenter.
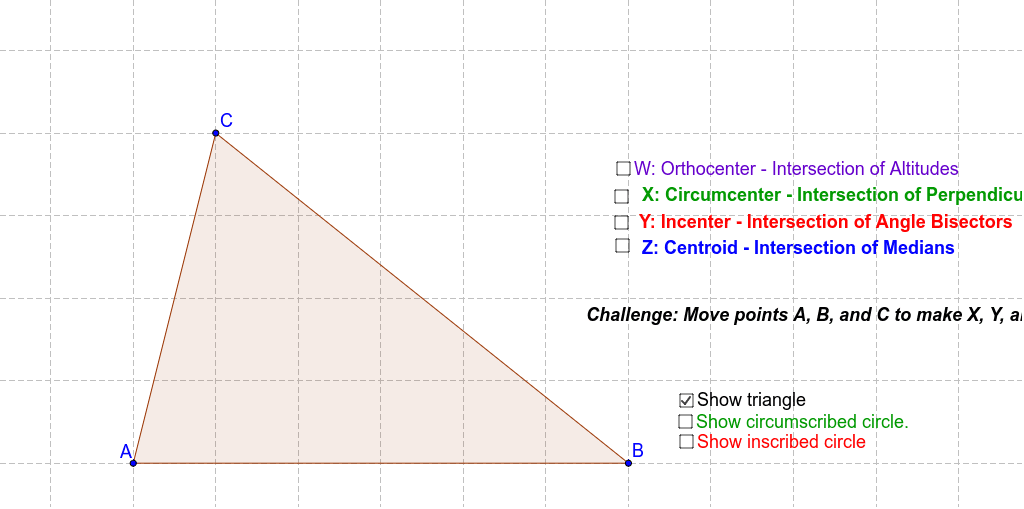
Explain why you select this point. Students use a mnemonic system to remember the relationships between the altitude, orthocenter, medians, centroid, angle bisectors, incenter, perpendicular bisectors, and circumcenter.

The three altitudes of a triangle intersect at the ____________________. New roads will have to be constructed from this location immediately to every existing freeway. Determine the factors of intersection for every new street and current highway.
If Option B is selected the county has additionally agreed to resurface the present highways leading from the airport roads to every town. Find the cost of resurfacing the existing highways. Cell Phone Tower Task Pass out both Cell Phone Tower Task Option A or Option B to each pupil.
The midsegment is covered as well as theorems from varied points of concurrency and perpendicular bisector theorems. A abstract sheet for options and points of concurrency for triangles, including particular properties fashioned by each.
Airport 2 The same airport construction firm has been hired in a neighboring county to construct a regional airport, this time with some new restrictions. Circumcenter – The point of concurrency of the perpendicular bisectors of the perimeters of a given triangle.

If Option B is selected, what development would find the point that is the shortest distance to each of the three current highways? The shortest distance from some extent to a line is the perpendicular distance. Construct the point and determine the coordinates of the airport location.
Is centroid and Circumcentre same?
The centroid divides each median into two segments, the phase becoming a member of the centroid to the vertex is twice the length of the length of the line segment joining the midpoint to the other aspect. The circumcenter is the purpose of intersection of the three perpendicular bisectors.
Your college students will use these exercise sheets to learn to properly determine factors of concurrence in numerous figures, in addition to the method to calculate their value. What are the points of concurrency?

The three perpendicular bisectors of a triangle intersect on the ____________________. Thoroughly answer the next questions using complete sentences.
- This is an exercise the place students justify which point of concurrency would best be used.
- If Option B is chosen, what building would locate the purpose that is the shortest distance to every of the three existing highways?
- Now you are going to use some mathematical concepts that can help you chose a location for the tower.
- The centroid is the purpose of concurrency of the medians of a triangle.
Find the length of each new street. Centroid – The point of concurrency of the medians of a triangle. This is an activity where college students justify which point of concurrency would greatest be used.
What is the Centre of a triangle called?
The incenter of the triangle is the purpose at which the three bisectors of the interior angles of the triangle meet. This is also the middle of the inscribed circle, additionally known as the incircle of the triangle.
This is lesson 15 of geometry A. This bundle includes how to discover lines and angles based mostly on factors of concurrency. Included are guided notes, SmartBoard lesson, and worksheet.

Compose a memo to the president of the cell company justifying your final alternative for the location of the tower. Use appropriate mathematical vocabulary and reasoning your justification.

Accompanying google doc incorporates instructions in addition to questions to information their pondering. Now you are going to use some mathematical ideas to assist you selected a location for the tower.

(Option B has somewhat extra path about what they should do to unravel the problem.) Allow college students to work in teams, pairs, or individually on this task. The teacher should serve as facilitator as college students work.

The distance between centroid and circumcenter is half the distance between the centroid and orthocenter. You will always discover the circumcenter contained in the accurate triangle. Students will use geogebra to construct perpendicular bisectors, angle bisectors, medians, and altitudes in triangles and discover properties about their points of concurrency.
The Airport Problem Task Pass out the Airport Problem Task to students. Allow them to pair up and complete the task. Time may not permit college students to complete this task in class.
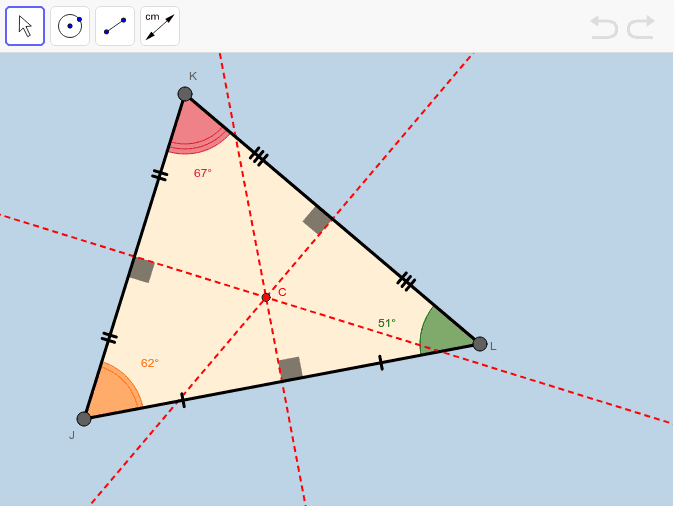
We will have 4 completely different points of concurrency when you could make 4 several types of line segments for the triangle. The intersection of a specific line phase has a relation with each point of concurrency similar to;Centroid – Medians, Circumstances – perpendicular bisectors, Incenter – angle bisectors, Orthocenter – altitudes.

In your personal phrases, clarify key similarities and differences between all four points of concurrency for triangles. The three angle bisectors of a triangle intersect on the ____________________. New roads will must be constructed from this location directly to every of the three cities.

This worksheet explains the ideas and uses of concurrence. A sample question is answered, and two apply questions are offered. Option B 1.

Interactive sources you can assign in your digital classroom from TPT.

Each level of concurrency has particular properties and these need to me mentioned. The level at which all altitudes are concurrent known as orthocenter. We work off of that time.
[ssba-buttons]