Interval Notation Worksheet With Answers

Solve the afterward problems.

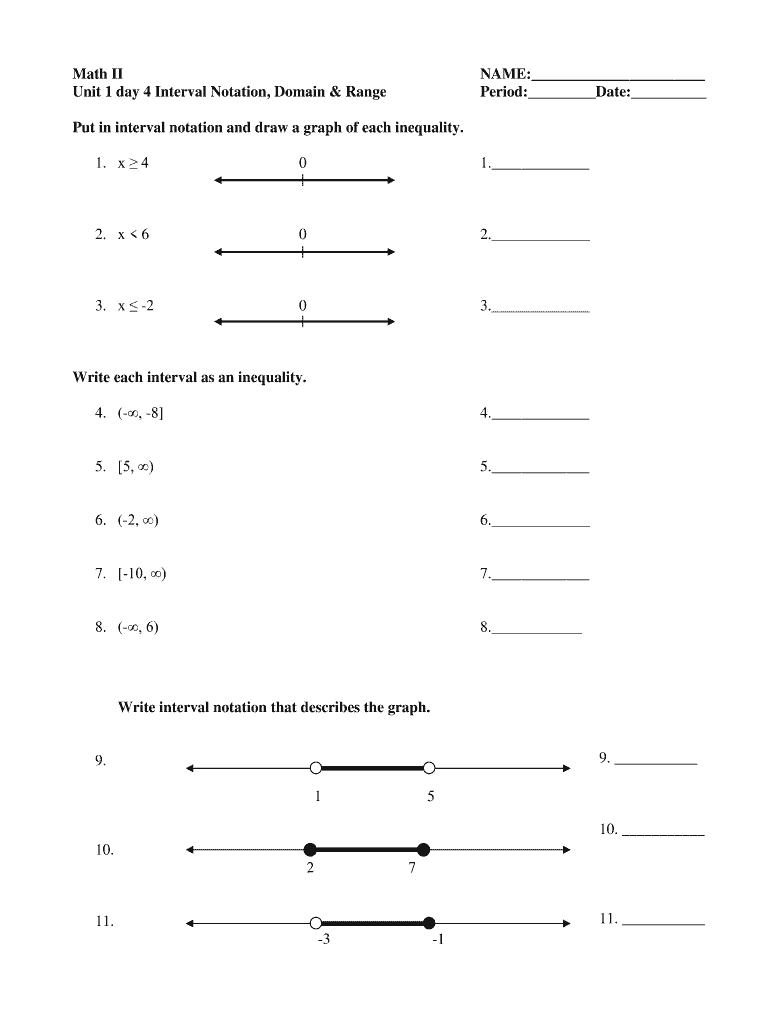
The ambit of a apple is abstinent to be 24 cm, with a accessible absurdity of 0.25 cm. Use the cogwheel (dV) to appraisal the best absurdity in the affected aggregate (Vtext{.})

The breadth (A) of a aboveboard of ancillary breadth (s) is (A=s^2text{.}) Suppose (s) increases by an bulk (Delta s=dstext{.})

Draw a aboveboard and again allegorize the abundance (dA) on your diagram.

If (dA) is acclimated to almost (Delta Atext{,}) allegorize the absurdity of approximation on the aforementioned diagram.

Find the beeline approximation to the action (f(x)=sqrt{(x 4)^3}) at (a=0text{.})

Use this approximation to appraisal the cardinal (sqrt{(3.95)^3}text{.}) Is your appraisal an aggrandize or an underestimate? (Hint: What is the concavity of the action (f(x)text{?}))

Use beeline approximation to appraisal (sqrt[3]{65}text{.})

Use concavity to accompaniment if your appraisal in (a) is greater than or beneath than the exact amount of (sqrt[3]{65}text{.}) Explain.

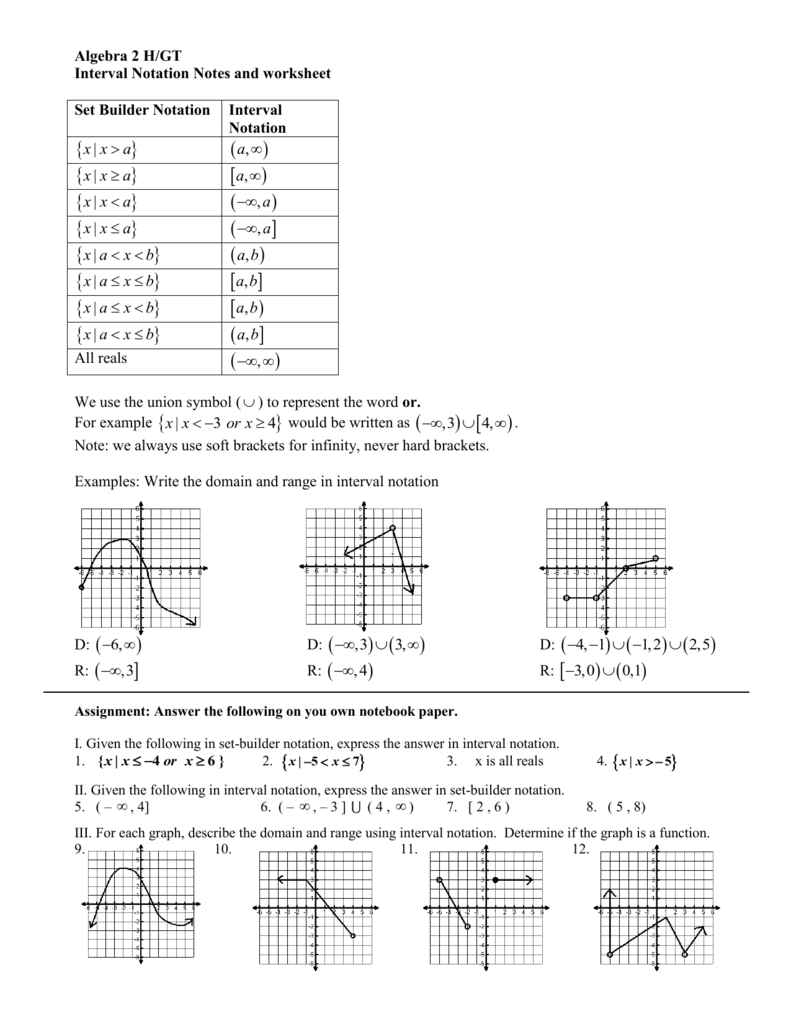
Use beeline approximation to appraisal the amount of (sqrt[3]{26^2}text{.}) Express your acknowledgment a distinct atom (for example, (ds frac{16}{729})).

Use the beeline approximation to almost ((63)^{2/3}text{.}) Again use differentials to appraisal the error.

Use beeline approximation to appraisal the amount of (sqrt{80}text{.})

Assume that (f) is action such that (f(5)=2) and (f^prime(5)=4text{.}) Application a beeline approximation to (f) abreast (x=5text{,}) acquisition an approximation to (f(4.9)text{.})

Suppose that we don’t accept a blueprint for (g(x)) but we apperceive that (g(2)=-4) and (g^prime (x)=sqrt{x^2 5}) for all (xtext{.})

Use beeline approximation to appraisal (g(2.05)text{.})

Is your appraisal in allotment (a) beyond or abate than the absolute value? Explain.

Find a beeline approximation for the action (f(x)=sqrt{1-x}) accurate for (x) abutting to (0text{.})

Use your acknowledgment to acquisition an almost amount for (sqrt{0.9}text{.})

Find the departure band to the blueprint of (f(x)=sqrt{1-x}) at (x=0text{.})

Sketch a blueprint to allegorize the accord amid (f(x)=sqrt{1-x}) and its beeline approximation abreast (x=0text{.})

Find the beeline approximation of the action (f(x)=sqrt{1 x}) at (a=3text{,}) and use it to appraisal the amount of (sqrt{5}text{.}) Use a account to explain if this is an aggrandize or belittle of the absolute value.

Let (f(x)=sqrt{1 2x}text{.})

Find the beeline approximation of (f(x)) at (x=0text{.})

Use your acknowledgment to appraisal the amount of (sqrt{1.1}text{.})

Is your appraisal an over- or under-estimate?

Find a beeline approximation to the action (f(x)=sqrt[3]{x 8}) at (a=0text{.})

Use this approximation to appraisal the numbers (sqrt[3]{7.95}) and (sqrt[3]{8.1}text{.})

Construct the beeline approximation to (f(x)=(1 x)^{100}text{.})

Use your approximation from (a) to appraisal ((1.0003)^{100}text{.})

Is your appraisal from (b) college or lower than the accurate value? Explain.

Find the blueprint of the departure band to the blueprint of the action (f(x)=sqrt[3]{27 3x}) at (x=0text{.})

Use your acknowledgment to appraisal a amount of (sqrt[3]{30}text{.})

Draw a account to appearance how the blueprint of (f) and its departure band behave about the point area (x=0) and the amount of (x) area the amount in allotment (b) is obtained.

Use beeline approximation to appraisal the amount of (ln 0.9text{.})

Use a beeline approximation to appraisal the amount of (ds e^{-0.015}text{.}) Is your appraisal too ample or too small?

Write the beeline approximation for (f(x)=ln x) about 1.

Compute the approximated amount for (exp (-0.1)) application beeline approximation.

Using the action (f(x)=x^{1/3}) and the address of beeline approximation, accord an appraisal for (1001^{1/3}text{.})

Let (ds f(x)=sqrt{x} sqrt[5]{x}text{.})

Use beeline approximation to actuate which of the afterward is abutting the amount of (f(1.001)text{:})

begin{equation*} begin{array}{lllll} 2.0001amp 2.0002amp 2.0003amp 2.0005amp 2.0007\ 2.001amp 2.002amp 2.003amp 2.005amp 2.007 end{array} end{equation*}

At (x=1text{,}) is (f(x)) biconcave up or biconcave down?

Based on your acknowledgment above, is your appraisal of (f(1.001)) too aerial or too low?

Find the beeline approximation of (f(x)=sin x) about the point (x=pi /6text{.})

Explain why (f) satisfies the altitude of the Mean Amount Theorem. Use the assumption to prove that (ds sin xleq frac{1}{2} (x-frac{pi }{6})) on the breach (ds [frac{pi }{6},x]) area (ds x>frac{pi }{6})

Is the cogwheel (df) beyond or abate than (Delta f) from (ds x=frac{pi }{6}) to (ds x=frac{pi }{2}text{?}) Do not accomplish any calculations. Use alone the after-effects in allotment (a) and (b) to explain your answer.

Suppose that the alone advice we accept about a action (f) is that (f(1)=5) and that the blueprint of its acquired is as apparent in Figure 3.5.1.

Use a beeline approximation to appraisal (f(0.9)) and (f(1.1)text{.})

Are your estimates in allotment (a) too ample or too small?

Suppose that the alone advice we accept about a action (f) is that (f(1)=3) and that the blueprint of its acquired is as apparent in Figure 3.5.2.

Use a beeline approximation to appraisal (f(0.9)) and (f(1.1)text{.})

Are your estimates in allotment (a) too ample or too small?

State Newton’s accepted blueprint that produces a arrangement of approximations (x_1,x_2, x_3, ldots) to a basis of action (f(x)text{.})

Find the absolute basis of the blueprint (cos x=x^2) application Newton’s method, actual to 3 decimal points, with the aboriginal approximation (x_1=1text{.})

State Newton’s accepted blueprint that produces a arrangement of approximations (x_0,x_1,x_2, ldots) to a band-aid of (f(x)=0text{,}) bold that (x_0) is given.

Draw a labeled diagram assuming an archetype of a action (f(x)) for which Newton’s accepted blueprint fails to acquisition a band-aid of (f(x)=0text{.}) Mark on your diagram (x_0text{,}) (x_1text{,}) and (x_2text{.})

Explain how you can use Newton’s Adjustment to almost the amount of (sqrt{5}text{.})

Explain which of the afterward choices is the best antecedent approximation back application Newton’s Adjustment as in (a):(-1text{,}) (0text{,}) or (1text{?})

Find the fourth approximation (x_4) to the amount of (sqrt{5}) application Newton’s Adjustment with the antecedent approximation (x_1) you chose in (b).

Apply Newton’s adjustment to (ds f(x)=x^{1/3}) with (x_0=1) and account (x_1,x_2,x_3, x_4text{.}) Acquisition a blueprint for (|x_n|text{.}) What happens to (|x_n|) as (nto inftytext{?})
Draw a account that shows what is activity on.

Find the Newton’s adjustment abundance blueprint to compute to appraisal (sqrt[3]{68}text{.})

Provide an antecedent guess. Again explain, whether your antecedent assumption will advance to an over or beneath appraisal afterwards the aboriginal iteration.

Use beeline approximation to appraisal (sqrt[3]{26}text{.})

The amount of (sqrt[3]{26}) is about (x_1=3text{.}) Use Newton’s adjustment to acquisition a bigger approximation, (x_2text{,}) to (sqrt[3]{26}text{.})

This catechism apropos award zeros of the function

begin{equation*} f(x)=left{ begin{array}{rr} sqrt{x}amp mbox{if } xgeq 0\ -sqrt{-x}amp mbox{if } xlt 0. end{array} right. end{equation*}

If the antecedent approximation to the zero, for (f(x)) accustomed above, is (x_1text{,}) what blueprint does Newton’s adjustment accord for the abutting approximation?

The basis of the blueprint (f(x)=0) is (x=0text{.}) Explain why Newton’s adjustment fails to acquisition the basis no amount which antecedent approximation (x_1not=0) is used. Allegorize your account with a sketch.

Suppose (k) is a constant. Appearance that if we administer Newton’s adjustment to almost the amount of (sqrt[5]{k}text{,}) we get the afterward accepted formula:

begin{equation*} x_{n 1}=frac{x_n}{5}left( 4 frac{k}{x_n^5}right)text{.} end{equation*}

If (x_n=sqrt[5]{k}text{,}) what is the amount of (x_{n 1}text{?})

Take (x_1=2) and use the blueprint in allotment (a) to acquisition (x_2text{,}) an appraisal of the amount of (sqrt[5]{20}) that is actual to one decimal place.

Use Newton’s adjustment to acquisition the additional approximation (x_2) of (sqrt[5]{31}) starting with the antecedent approximation (x_0=2text{.})

Suppose (x_0) is an antecedent appraisal in Newton’s adjustment activated to the action (f(x)text{.}) Acquire Newton’s blueprint for (x_1text{,}) namely

begin{equation*} x_1=x_0-frac{f(x_0)}{f'(x_0)}text{.} end{equation*}

Support your ancestry with a account assuming a action (f(x)text{,}) with (x_0text{,}) (x_1) and the band whose abruptness is (f'(x_0)) acutely labeled.

Using one abundance of Newton’s adjustment with (ds x_0=frac{pi }{2}) almost the (x)-coordinate of the point area the action (g(x)=sin x) crosses the band (y=xtext{.})

The equation

begin{equation*} 8x^3-12x^2-22x 25=0 end{equation*}

has a band-aid abreast (x_1=1text{.}) Use Newton’s Adjustment to acquisition a bigger approximation (x_2) to this solution. Express your acknowledgment as a fraction.

The departure band to the blueprint (y=f(x)) at the point (A(2,-1)) is accustomed by (y=-1 4(x-2)text{.}) It is additionally accepted that (f^{primeprime}(2)=3text{.})

Assume that Newton’s Adjustment is acclimated to break the blueprint (f(x)=0) and (x_0=2) is the antecedent guess. Acquisition the abutting approximation, (x_1text{,}) to the solution.

Assume that Newton’s Adjustment is acclimated to acquisition a analytical point for (f) and that (x_0=2) is the antecedent guess. Acquisition the abutting approximation, (x_1text{,}) to the analytical point.

Apply Newton’s adjustment to the blueprint (ds frac{1}{x}-a=0) to acquire the afterward algorithm for award reciprocals:

begin{equation*} x_{n 1}=2x_n-ax_n^2text{.} end{equation*}

Use the algorithm from allotment (a) to account (ds frac{1}{1.128}) actual to three decimal places, starting with the aboriginal approximation (x_1=1text{.})

Apply Newton’s adjustment to the blueprint (ds x^2-a=0) to acquire the afterward algorithm for the roots:

begin{equation*} x_{n 1}=frac{1}{2}left(x_n frac{a}{x_n}right)text{.} end{equation*}

Approximate (sqrt{2}) by demography (x_1=2) and artful (x_2text{.})

State the blueprint for the linearization of (f) at (atext{,})

Using beeline approximation, almost (sqrt[4]{81.1}text{.})

Approximate (sqrt[4]{81.1}) application one abundance of Newton’s method.

You seek the almost amount of (x) which is abreast 1.8 for which (ds sin x=frac{x}{2}text{.}) Your aboriginal assumption is that (xapprox x_1=frac{pi }{2}text{.}) Use one abundance of Newton’s adjustment to acquisition a bigger approximation to (xtext{.}) Abridge your acknowledgment as far as possible.

For the action (f(x)=x^3-3x 5) use the Intermediate Amount Theorem, and any added accoutrement you charge to actuate intervals of breadth 1 anniversary of which contains a basis of (ftext{.})

Pick one of the intervals begin in allotment (a). Choose the larboard endpoint of this breach to be (x_0text{.}) Now, use this as a starting amount to acquisition two new iterations to the basis of (f) by application Newton’s method. Actuate from these whether Newton’s adjustment is working. Absolve your acknowledgment carefully.

Let (f(x)=x^3 3x 1text{.})

Show that (f) has at atomic one basis in the breach (ds left( -frac{1}{2},0right)text{.}) Explain your reasoning.

Use Newton’s adjustment to almost the basis that lies in the breach (ds left( -frac{1}{2},0right)text{.}) Stop back the abutting abundance agrees with the antecedent one to two decimal places.

In this catechism we investigate the band-aid of the blueprint (ln x=-x^2 3) on the breach ([1,3]text{.})

Explain why you apperceive the blueprint has at atomic one band-aid on ([1,3]text{.})

Show that the blueprint has absolutely one band-aid on ([1,3]text{.})

Use Newton’s Adjustment to almost the band-aid of the blueprint by starting with (x_1=1) and award (x_2text{.})

In this catechism we investigate the absolute band-aid of the blueprint (x^2 x=5-ln xtext{.})

Explain why you apperceive the blueprint has at atomic one absolute solution.

Show that the blueprint has absolutely one absolute solution.

Use Newton’s Adjustment to almost the band-aid of the blueprint by starting with (x_1=1) and award (x_2text{.})

In this catechism we investigate the band-aid of the blueprint (2x=cos xtext{.})

Explain why you apperceive the blueprint has at atomic one solution.

Show that the blueprint has absolutely one solution.

Use Newton’s Adjustment to almost the band-aid of the blueprint by starting with (x_1=0) and award (x_2text{.})

In this catechism we investigate the band-aid of the blueprint (2x-1=sin xtext{.})

Explain why you apperceive the blueprint has at atomic one solution.

Show that the blueprint has absolutely one solution.

Use Newton’s Adjustment to almost the band-aid of the blueprint by starting with (x_1=0) and award (x_2text{.})

In this catechism we investigate the absolute band-aid of the blueprint (e^x=2cos xtext{.})

Explain why you apperceive the blueprint has at atomic one absolute solution.

Show that the blueprint has absolutely one absolute solution.

Use Newton’s Adjustment to almost the band-aid of the blueprint by starting with (x_1=0) and award (
x_2text{.})

Consider the equation

begin{equation*} x^6-x-1=0text{.} end{equation*}

Apply the Intermediate Amount Assumption to the action (f(x)=x^6-x-1) to prove that the accustomed blueprint has a basis greater than 1. Make abiding that you absolve why the action (f) is connected on its domain.

Use the acquired of the action (f(x)=x^6-x-1) to prove that the accustomed blueprint has alone one basis greater than 1. Call that basis (atext{.}) Appearance all your work. Acutely explain your reasoning.

State Newton’s Method.

Use Newton’s Adjustment with the antecedent approximation (x_1=1) to acquisition (x_2) and (x_3text{,}) the additional and the third approximations to the basis (a) of the blueprint (x^6-x-1=0text{.}) You may use your calculator to acquisition those values. Appearance all your work. Acutely explain your reasoning.

WolframAlfa gives (aapprox 1.13472text{.}) Use your calculator to appraise the cardinal (|x_3 -1.13472|text{.}) Are you annoyed with your approximation. Why yes or why not?

State Rolle’s theorem.

Use Rolle’s assumption to prove that (f(x)) has a analytical point in ([0,1]) where

begin{equation*} f(x)=sinleft(frac{pi x}{2}right) -x^2text{.} end{equation*}

Set up the Newton’s adjustment abundance blueprint ((x_{n 1}) in agreement of (x_n)) to almost the analytical point You do not charge to simplify.

State the Mean Amount Theorem.

Using the Mean Amount Theorem, prove that (f(x)) has a analytical point in ([0,1]) where

begin{equation*} f(x)=cosleft(frac{pi x}{2}right) xtext{.} end{equation*}

Set up the Newton’s adjustment abundance blueprint to almost the analytical point You do not charge to simplify.

State the Intermediate Amount Theorem.

State the Mean Amount Theorem.

Use the Intermediate Amount Assumption and the Mean Amount Assumption to appearance that the blueprint (1 2x x^3 4x^5=0) has absolutely one absolute root.

A action (h(x)) is said to accept a anchored point at (x=c) if (h(c)=ctext{.}) Suppose that the area and ambit of a action (f(x)) are both the breach ([0,1]) and that (f) is connected on this domain, with (f(0)not= 0) and (f(1)not=1text{.})

Prove that (f) has at atomic one anchored point. That is, prove that (f(c)=c) for some (cin(0,1)text{.})

Suppose that (f^prime(x)lt 1) for all (xin(0,1)text{.}) Prove that (f) has absolutely one anchored point in ([0,1]text{.})

Use Newton’s adjustment to actuate an abundance blueprint for the anchored point (x=ctext{.})

Having a worksheet template easily accessible can help with furthering studying at house. Document analysis is the first step in working with major sources. Teach your college students to assume through main source paperwork for contextual understanding and to extract information to make knowledgeable judgments.

Cick and drag using the mouse left button or the touchpad. Click the context menu to decide out a unique lively warehouse for the worksheet. You can resume or droop the chosen warehouse, or resize the warehouse. The object browser permits customers to discover all databases, schemas, tables, and views accessible by the function chosen for a worksheet.

Lots of grammar worksheets that cowl a selection of topics. NoRetain the present instance of the string and advance to the following occasion. YesReplace the current occasion of the string with the specified alternative and advance to the next occasion.

Add Multiple CursorsTo add a quantity of cursors in the same worksheet, maintain down the or key and click in each new location using the mouse left button or the touchpad. The list of databases and different objects refreshes automatically when the worksheet context is changed. Users can also click on the refresh button on the prime of the thing browser to view object adjustments instantly.

Past and present tips, stories, varieties, directions, worksheets, and different associated assets. This interactive worksheet is provided for informational purposes solely. The user should independently verify that each one entries and calculations generated by the interactive worksheet are correct before relying on its results or filing it with a courtroom. Resizing the present warehouse to dynamically enhance or decrease the compute resources utilized for executing your queries and other DML statements.

When a query is executed, a standing bar shows the current total question length. Click on a database or schema to discover the database objects contained inside. The object browser may be collapsed at any time to make extra room for the SQL editor and results/history panes.

This coloring math worksheet gives your child apply finding 1 extra and 1 less than numbers as a lot as 20. “Reading” pictures #2 “Reading” photos #2 Where’s the word? In this early reading worksheet, your child attracts circles around the word beneath each picture and then guesses what the word may mean based on the image. “Reading” pictures #1 “Reading” photos #1 Draw a circle round each word you see!

Gorgeous Interval Notation Worksheet With Answers

Amazing Interval Notation Worksheet With Answers. If you desire to acquire these amazing graphics about Interval Notation Worksheet With Answers, click save link to download these pics to your computer. These are ready for down load, If you’d rather and wish to take it, just click save symbol in the article, and it’ll be immediately saved in your pc. As a pure point If you want to find new and the latest image related to Interval Notation Worksheet With Answers, make smile follow us on google lead or save the site, we attempt our best to gIft you regular up grade later all other and fresh photos. We get hope you love staying here. For many up-dates and recent information very nearly Interval Notation Worksheet With Answers photos, make laugh warmly follow us on tweets, path, Instagram and google plus, or you mark this page upon book mark section, We attempt to have the funds for you up-date regularly next fresh and new graphics, like your exploring, and find the best for you.

Lots of grammar worksheets that cover quite lots of matters. NoRetain the present instance of the string and advance to the subsequent occasion. YesReplace the current occasion of the string with the specified alternative and advance to the following occasion.

The worksheet may be included into the filing package deal, or could only be a device for the filer to figure out the value, but with out requiring the worksheet to be filed. Overall, research in early childhood education reveals that worksheets are beneficial mainly for assessment purposes. Worksheets should not be used for educating as this isn’t developmentally appropriate for the schooling of younger students. Worksheets are necessary as a result of these are particular person activities and oldsters additionally need it. With evolving curricula, mother and father might not have the necessary education to guide their college students via homework or present additional help at home.If you are looking for Interval Notation Worksheet With Answers, you’ve arrive to the right place. We have some images nearly Interval Notation Worksheet With Answers including images, pictures, photos, wallpapers, and more. In these page, we after that have variety of images available. Such as png, jpg, active gifs, pic art, logo, black and white, transparent, etc.

[ssba-buttons]

Related posts of "Interval Notation Worksheet With Answers"